Linear Algebra Bootcamp

Not Completed…

Vectors

Definition: A vector is a geometric object that has magnitude and direction (e.g. force, velocity, acceleration, and momentum). It is useful to represent vectors in terms of coordinates:

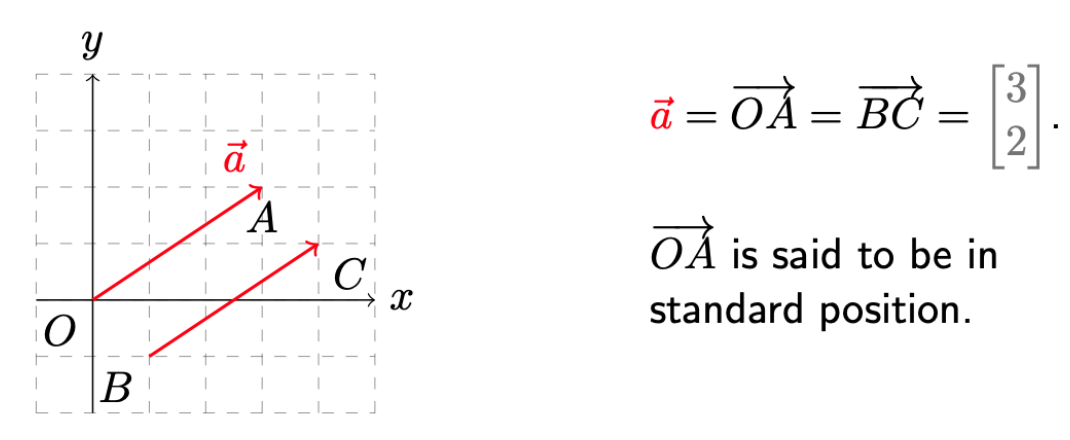
An example of Vectors.

Vector Operations:Vectors can be scaled, added, and substracted.

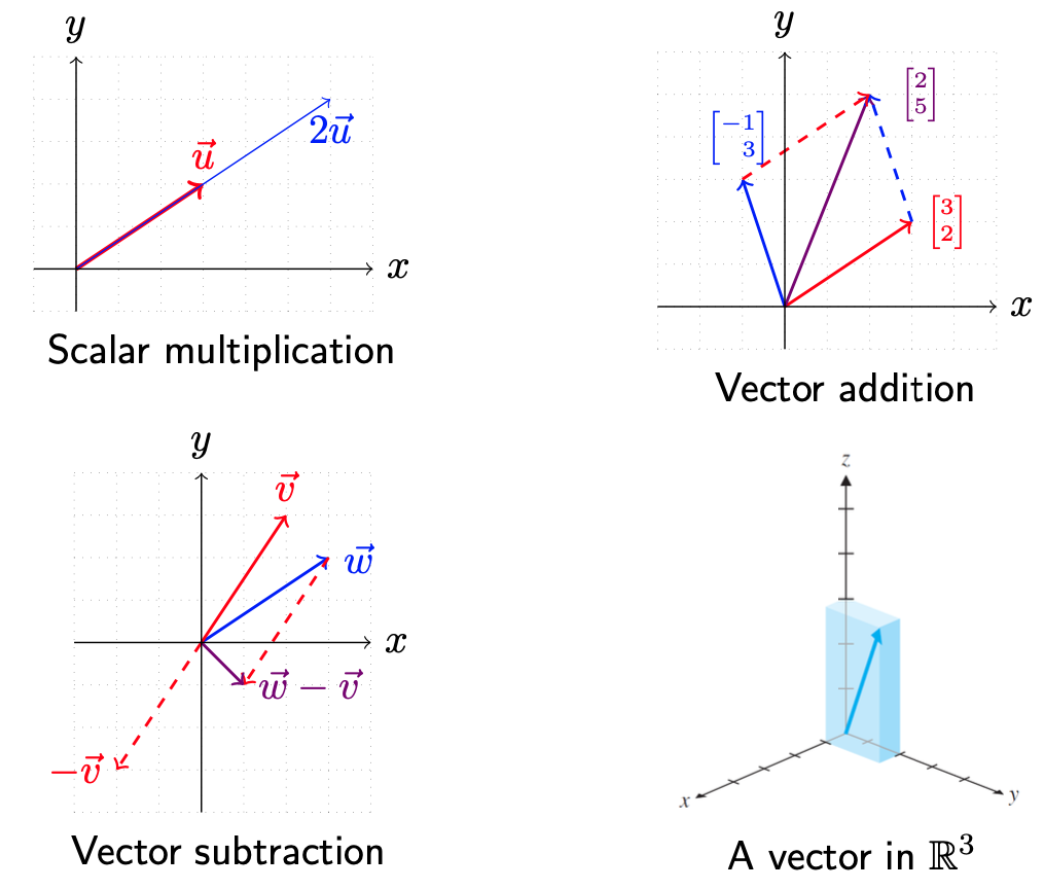
Vector Operations.

Vector Length: The length of a vector \(x\in \mathbb{R}^n\) is: \(\|x\| = \sqrt{\sum_{i=1}^n{x_i^2}}\)

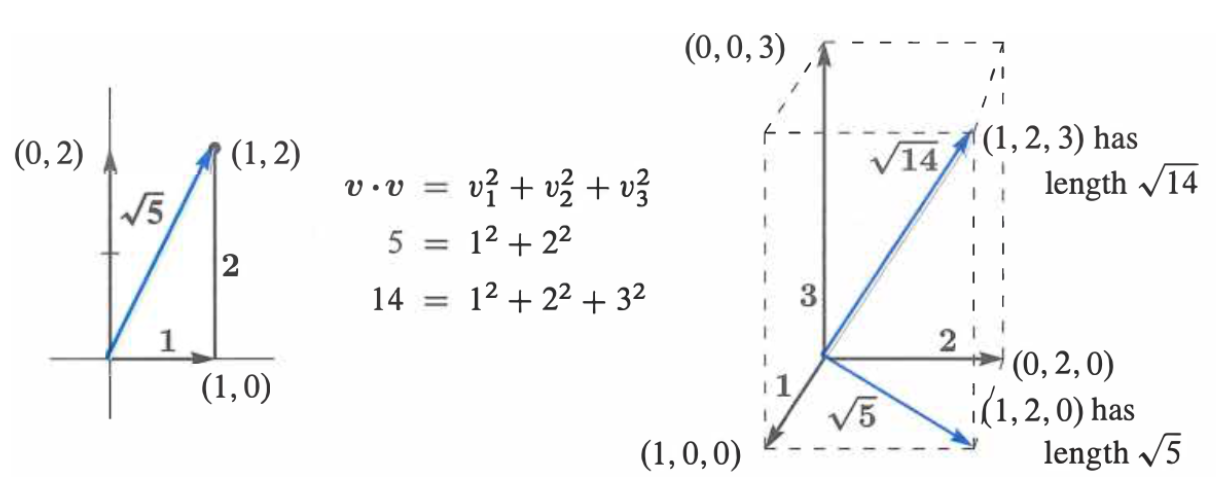
An example of Vector Length.

Inner Product: The inner product of \(x, y \in \mathbb{R}^n\) is given by:

\[\langle x, y \rangle = \sum_{i=1}^nx_iy_i\]

Esspecially, the relationship between length and inner product is \(\|x\|^2 = \langle x, x \rangle\)

Projections of Vectors: The projection of a vector \(u\) on a nonzero vector \(v\), is the unique vector in the direction of \(v\) that is closest to \(u\), and is given by

\[\text{proj}_v(u) = \frac{\langle u, v \rangle}{\|v\|^2}v\]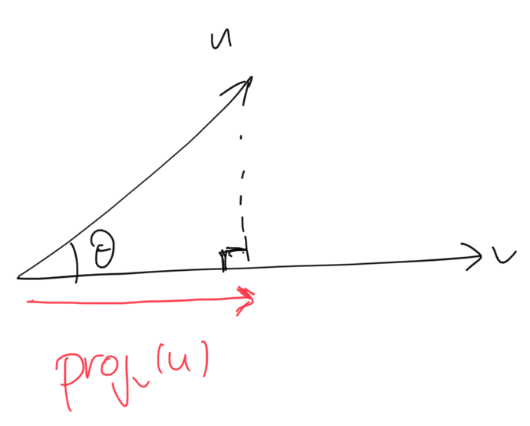

An example of Vector Projection.

Note: The length of the projection is \(\frac{\langle u, v \rangle}{\|v\|^2}\)

Angle between two vectors: the angle between \(x, y \in \mathbb{R}^n\) is defined as

\[\theta = \arccos{\frac{\langle x, y \rangle}{\|x\|\|y\|}}\]

Linear Subspace: A subset \(S \subseteq \mathbb{R}^N\) is a (real) subspace if it is closed under addition and scalar multiplication, i.e.

\[x, y \in S, \lambda, \mu \in \mathbb{R} \Rightarrow \lambda x + \mu y \in S\]

These are not Linear Subspace. The left and middle are not true because of the scalar multiplication, the right is not true because of the addition.

These is a Linear Subspace.

Linear span of a set: For a set \(A \subseteq \mathbb{R}^n\) define

\begin{aligned} span(A) & = \bigcap \{S: S \text{ is a subspace of } \mathbb{R}^n \text{containing} A\}\\ & = \text{the smallest subspace of } \mathbb{R}^n \text{containing} A \end{aligned}

In particular, the span of a single vector is the line spanned by it whereas the span of two vectors is the plane spanned by them.

Note: The intersection of subspaces is a subspace.

Linear Combination: Given vectors \(a_1,\dots, a_m \subseteq \mathbb{R}^n\) and \(\lambda_1, \dots, \lambda_m \in \mathbb{R}\), the vector

\[\lambda_1a_1 + \dots + \lambda_ma_m\]

is called a linear combination of \(a_1, \dots, a_m\)

Especially, The set of all linear combinations of elements in \(A\) is \(span(A)\), i.e.

\[span(A) = \left\{ \sum_{i=1}^k\lambda_ia_i: a_i \in A, k\in\mathbb{N}\right\}\]

Linear Independence: The vectors \(a_1, \dots, a_m\) linearly independent if no vector lies in the span of the others, i.e.,

\[a_i \notin span(a_j: j \neq i) \forall i\]

Example:

• \(a_1, a_2\) are linearly independent if they are not parallel
• \(a_1, a_2, a_3\) are linearly independent if \(a_1 \notin span(a_2, a_3)\) and similarly for \(a_2, a_3\)

Note: The max number of linearly independent points in \(\mathbb{R}^n\) is \(n\).

Checking Independence: The vectors \(a_1, \dots, a_m\) are linear independent if the homogeneous linear system

\[\left( a_1 \quad \cdots \quad a_m \right) \begin{pmatrix} \lambda_1 \\ \vdots \\ \lambda_n \end{pmatrix} = 0\]

has only one solution \(\lambda_i=0 \forall i\).